Contents
Introduction
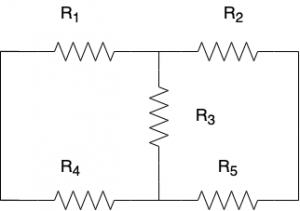
There is a special type of circuit network which is neither in parallel or in series. Usual methods such as combining resistors in series or parallel does not work. Consider the network in Figure 1.
Resistor \(R_3\) which is in between resistors \(R_1\),\(R_2\) and \(R_4\),\(R_5\) causes trouble to compute the total resistance seen in this network (which is \((R_1+R_2)||(R_4+R_5)\) if \(R_3\) is not present). To tackle this problem, we need to transform this network into a network where we can apply the series/parallel combination. This transformation is called the wye-delta transformation.
Figure 1: Network with \(R_3\) in the middle.
Wye-Delta configuration
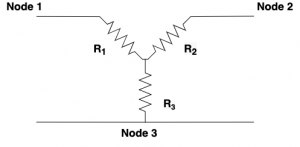
Figure 2. Wye network
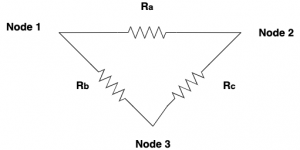
Figure 3. Delta network
It is useful to remember the above two network configuration, should you come across them in a circuit. Once identified, the wye \(Y\) network might need to be transformed into a delta \(\Delta\) network, or vice versa to compute equivalent resistance.
Delta to Wye Transformation
Figure 4. Superimposed Wye and Delta network for the purpose of deriving their transformation
The delta network consists of \(R_a\),\(R_b\),\(R_c\) and we want to find the equivalent wye network \(R_1\),\(R_2\),\(R_3\)
In the delta network, the resistance between node 1 and node 2 is
\[R_{12}(\Delta) = R_a+(R_b||R_c)\]
Similarly for the Y network the resistance between node 1 and node 2 is
\(R_{12}(Y) = R_1+R_2\)
Equating \(R_{12}(\Delta) = R_{12}(Y)\) yields
\[R_a+(R_b||R_c) = R_1+R_2\]
\[\frac{R_a(R_b+R_c)}{R_a+R_b+R_c} = R_1+R_2 \tag{1}\]
Equation \((1)\) can also be similarly done for nodes 1,3 and nodes 2,3. It is left to reader to verify these
\[\frac{R_b(R_a+R_c)}{R_a+R_b+R_c} = R_1+R_3 \tag{2}\]
\[\frac{R_c(R_a+R_b)}{R_a+R_b+R_c} = R_2+R_3 \tag{3}\]
Subtracting \((1)\) from \((3)\) gives
\[R_1-R_3=\frac{R_a(R_b+R_c)}{R_a+R_b+R_c} – \frac{R_c(R_a+R_b)}{R_a+R_b+R_c}\]
\[R_1-R_3=\frac{R_aR_b+R_aR_c-R_aR_c-R_bR_c}{R_a+R_b+R_c}\]
\[R_1-R_3=\frac{R_aR_b-R_bR_c}{R_a+R_b+R_c} \tag{4}\]
To get rid of the \(R_3\) term, add \((2)\) with \((4)\)
\[R_1-R_3+R_1+R_3 = \frac{R_aR_b-R_bR_c+R_aR_b+R_bR_c}{R_a+R_b+R_c}\]
\[2R_1 = \frac{2R_aR_b}{R_a+R_b+R_c}\]
\[\boxed{R_1 = \frac{R_aR_b}{R_a+R_b+R_c}} \tag{5.a}\]
Both \(R_2\) and \(R_3\) can be similarly derived
\[\boxed{R_2 = \frac{R_aR_c}{R_a+R_b+R_c}} \tag{5.b}\]
\[\boxed{R_3 = \frac{R_bR_c}{R_a+R_b+R_c}} \tag{5.c}\]
Notice that the numerator of \(R_1\) is the product of its adjacent resistor \(R_a\) and \(R_b\)
Wye to Delta Transformation
To derive \(R_a\) in terms of \(R_1\),\(R_2\), and \(R_3\), take note of the following ratios derived from the delta-wye transformation in equation 5.a,5.b and 5.c. These ratios will be used to derive the wye-delta transformation.
\[\frac{R_1}{R_2} = \frac{R_b}{R_c}\]
\[\frac{R_2}{R_3} = \frac{R_a}{R_b}\]
\[\frac{R_1}{R_3} = \frac{R_a}{R_c}\]
Taking equation 5.a and dividing by \(R_b\) on both numerator and denominator of right hand side,
\[R_1 = \frac{R_aR_b}{R_a+R_b+R_c} \]
\[R_1 = \frac{R_a}{\frac{R_a}{R_b}+1+\frac{R_c}{R_b}} \]
\[R_1 = \frac{R_a}{\frac{R_2}{R_3}+1+\frac{R_2}{R_1}} \]
\[R_1 = \frac{R_a}{\frac{R_1R_2+R_2R_3 + R_1R_3}{R_1R_3}} \]
\[R_1\frac{R_1R_2+R_2R_3 + R_1R_3}{R_1R_3} = R_a \]
\[\boxed{R_a = \frac{R_1R_2+R_2R_3 + R_1R_3}{R_3}}\]
\(R_a\) and \(R_b\) can be derived similary
\[\boxed{R_b = \frac{R_1R_2+R_2R_3 + R_1R_3}{R_2}}\]
\[\boxed{R_c = \frac{R_1R_2+R_2R_3 + R_1R_3}{R_1}}\]